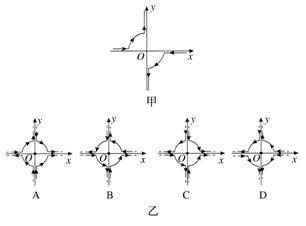
本題考察了兩根無限長導線在恒定電流i作用下的磁場分布情況。已知直線部分與坐標軸接近重合，彎曲部分是以坐標原點o為圓心、相同半徑的一段圓弧，且直線部分在原點附近。均四甲苯的提及可能為題目背景或干擾信息，與電磁場的核心計算無關。

根據安培環路定理，無限長直導線在空間任意點產生的磁感應強度大小為B = (μ?i)/(2πr)，方向由右手螺旋定則確定。對于直線部分沿坐標軸的情況，其在原點附近產生的磁場方向需根據電流方向具體分析。

彎曲部分為圓弧導線，可視為多個電流元的組合。根據畢奧-薩伐爾定律，圓弧電流在圓心處產生的磁感應強度大小為B = (μ?iθ)/(4πR)，其中θ為圓弧對應圓心角（弧度），R為圓弧半徑。方向垂直于圓弧平面，由右手定則判斷。

在本題中，由于兩根導線結構對稱且電流相同，需計算各部分在原點處的磁場矢量疊加：

1. 直線部分：若沿x軸和y軸布置，在原點處磁場可能相互抵消或增強，取決于電流方向。
2. 圓弧部分：若為四分之一圓弧或其他對稱結構，需根據實際圓心角計算貢獻。

最終，通過矢量合成即可得到原點處的總磁感應強度。計算時需注意單位統一，使用國際單位制。